Giới thiệu

Trong các bài toán machine learning, Seq2Seq là bài toán phổ biến cả trong NLP và CV, có input và output đều dạng chuỗi (sequence). Những bài toán Seq2Seq như Machine Translate, Auto Tagging, Speech to Text, Text to Speech, Handwriting recognition khá quen thuộc và hầu hết giải pháp tối ưu nhất cho những bài toán này đều dựa vào Deep learning. Trong đó có hai bài toán đặc biệt khó: Speech to Text và Handwriting recognition. Để hiểu được lý do tại sao, hãy quan sát ví dụ dưới đây:

Định nghĩa:

• Input là 1 chuỗi X = $[x_1, x_2, x_3,… x_T]$
• Output là chuỗi Y = $[y1, y2, y3, .. y_U]$
• T, U là biến số. Nói cách khác: độ dài X và Y là không cố định và thường khác nhau.
• Độ rộng mapping từng phần tử $x_i$ với $y_i$ không giống nhau. Trong bài toán nhận dạng chữ viết tay, các kí tự cạnh nhau có thể có nét đè lên nhau, overlap nhau… rất khó để chia ảnh input thành từng đoạn rõ ràng, tách biệt tương ứng từng kí tự.

Trước đây, trước khi có CTC người ta dùng các giải pháp để cố gắng tách chuỗi input thành từng đoạn tương ứng với $y_i$, tức cố gắng chia input sao cho độ dài chuỗi X bằng độ dài chuỗi Y. Tuy nhiên cách này không thực sự hiệu quả. CTC ra đời nhằm giải quyết những bài toán dạng này.

Ý tưởng CTC

Thay vì tìm cách phân chia input thành các đoạn tương ứng với từng $y_i$ (bước align) bằng các thuật toán tự định nghĩa, CTC sẽ tự học và làm việc đó. Hãy quan sát hình dưới đây.

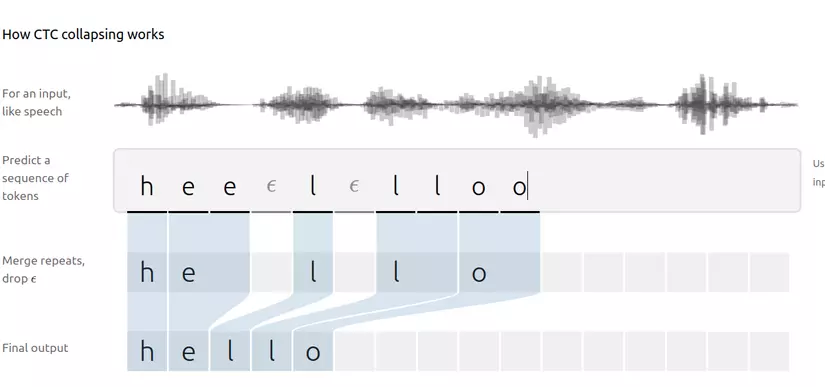
Input là một audio, giả sử audio này được chia thành 10 phần bằng nhau time_step = 10, label của audio là “hello”.

Thay vì tìm cách predict trực tiếp ra “hello”, ta sẽ predict ra các biến thể của nó là “hhheel_llo”, “h_e_ll_l_o”, … mỗi biến thể này ta gọi là một alignment. Độ dài của một alignment bằng với độ dài input = T ($=timesteps = 10$). Như vậy model deep learning nhận input đầu vào và output ra các alignment ( “hhheel_llo” hoặc h_e_ll_l_o, … ) tương ứng với nhãn “hello”. Từ các alignment, bằng việc loại bỏ các kí tự lặp ta thu được kết quả mong muốn. xác suất để predict ra “hello” bằng tổng xác suất tất cả alignment.

Tạo ra các alignment

Tạo các alignment cho “hello” bằng cách lặp lại các kí tự với sao cho len(y) = len(x) = T = 10. Có một vấn đề đặt ra là: giả sử model trả về output “heeeeellloo”, loại bỏ các kí tự lặp ta chỉ thu được “helo” thay vì “hello”.

Để giải quyết vấn đề này, ta sử dụng kí tự đặc biệt blank token - $ϵ$ (đừng nhầm với kí tự khoảng trắng, khoảng cách). $ϵ$ có thể được thêm vào bất kì chỗ nào trong chuỗi “hello”, và giữa hai kí tự giống nhau liền kề bắt buộc phải có $ϵ$ ở giữa. Như vậy, “hello” sẽ có các alignment: “heeeel–llo”, ‘-hell-l–oo’ … luôn có ít nhất một kí tự “-“ giữa hai kí tự “l” ( “-“ là biểu diễn cho $ϵ$)

Loss function

Đặt $A_{XY}$ là tập tất cả các alignment A của Y. xác suất model có thể predict ra Y với input X là tổng xác suất của tất cả A trong $A_{XY}$. Xác suất của A lại bằng tổng xác suất từng kí tự $a_t$ trong A. CTC loss chính là P(Y|X) trong hình:

Phương pháp tính P(Y|X) cải tiến

Note: Thuật toán này đọc hơi trìu tượng, hơi khó diễn tả, bạn có thể skip phần này. CTC_loss được hỗ trợ trong keras, tensorflow cho bạn dùng sẵn.

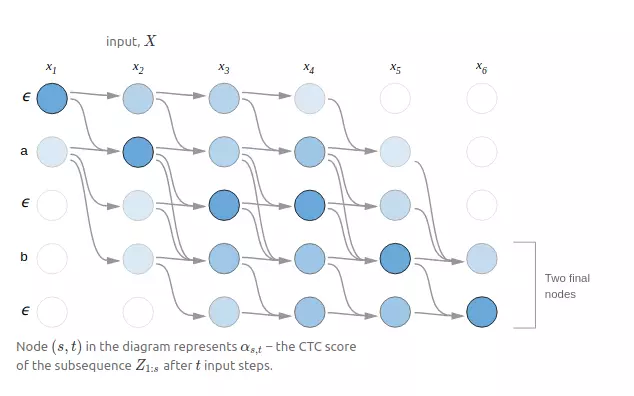
Về lý thuyết, ta cần thống kê ra tất cả alignment có thể có (kể cả đúng và sai). Giả sử với tập 9 kí tự, time_step = 10, số lượng tổ hợp lên tới $10^9$. Số lượng tổ hợp tăng cấp số nhân theo số lượng kí tự và time_step. Như vậy, việc liệt kê tất cả các alignment và tính tổng xác suất các alignment hợp lệ là việc không khả thi. Để cải thiện tốc độ, người ta đã sử dụng thuật toán dynamic programing, thuật toán như sau:

Do blank token $ϵ$ có thể xuất hiện tại bất kì vị trí nào trong chuỗi Y, để dễ dàng mô tả thuật toán, ta đặt target output là Z = $[ϵ, y_1, ϵ, y_2 … y_i, ϵ]$.

• Z được tạo từ label Y với các kí tự $ϵ$ xen giữa các kí tự $y_i$, length(Z) = S
• Đặt M = $[m_1, m_2, … m_t]$ là chuỗi output mà model tính toán và trả về. Length(M) = length(input) = T
• Đặt $p_{s,t}$ là xác suất để M[t] = Z[s]
• Đặt $a_{s,t}$ là xác suất tạo chuỗi Z[1:s] từ chuỗi M[1:t] thu gọn.
• Ví dụ target label Y = “hello” => Z = $[ϵ, h, ϵ, e, ϵ, l, ϵ, l, ϵ, o, ϵ]$. Kết quả cuối cùng model predict ra là chuỗi M = $[ϵ,h,ϵ,e,e,ϵ,l,l,ϵ,l,ϵ,o, ϵ]$. Ví dụ: $a_{4,5}$ là xác suất chuỗi gồm 5 kí tự đầu tiên $[ϵ,h,ϵ,e,e]$ trong chuỗi M trở thành chuỗi gồm 4 kí tự [$ϵ$, h, $ϵ$, e] trong chuỗi Z
• Tư tưởng của dynamic programing trong CTC loss là: nếu đã biết $a_{s,t}$ và $p_{s,t}$ ta có thể tính được $a_{s,t+1}$, $a_{s+1,t+1}$

Như vậy để tính CTC_loss, ta lần lượt tính $a_{1,1}$, $a_{1,2}$, $a_{2,1}$… để cuối cùng tính ra được $a_{s,t}$ cuối cùng với s=S, t=T. Trong quá trình tính $a_{s,t}$ tại 1 thời điểm bất kì, sẽ xảy ra 2 trường hợp:

Case 1

Case: Z[s-1] = $ϵ$ và nằm giữa hai kí tự giống nhau. Trong trường hợp này, kí tự $ϵ$ là kí tự không thể thiếu, bắt buộc phải có để phân biệt hai kí tự giống nhau. Vậy sẽ có hai trường hợp hợp lệ xảy ra taị thời điểm t-1 là: M[t-1] = Z[s-1] = $ϵ$ và M[t-1] = Z[s] (do Z[s-1] = $ϵ$ nên Z[s] != $ϵ$)

\[a_{s,t} = (a_{s-1,t-1} + a_{s,t-1} ) * p_{s,t}\]

Case 2

Case: Z[s-1] = $ϵ$ và nằm giữa hai kí tự khác nhau. Đặt hai kí tự này là b và c. Trong trường hợp này, kí tự $ϵ$ không còn quan trọng (tức không giữ vai trò phân biệt hai kí tự lặp) nên kết quả tính ra có thể không cần $ϵ$. Vậy tại 1 thời điểm t với M[t] = b, sẽ có 3 khả năng xảy ra tại thời điểm t-1:

• M[t-1] = c
• M[t-1] = $ϵ$
• M[t-1] = b (tương đương với trường hợp Z[s-1] != $ϵ$)

Vậy, $a_{s,t}$ được tính theo công thức:

\[a_{s,t} = (a_{s-2,t-1} + a_{s-1,t-1} + a_{s,t-1}) * p_{s,t}\]

Kết luận

Như vậy mình đã giới thiệu qua về tư tưởng của CTC. Dù hơi khó hiểu, mình vẫn hi vọng bài viết sẽ giúp bạn có cái nhìn rõ hơn chút về CTC. Cảm ơn bạn đã đọc bài viết.